量子もつれとは一体なんでしょうか?量子は、電子や光子などといったとても小さな粒子のことです。それがもつれるといわれても一体どういうことなのか、いまいちイメージできないですよね。ネット上でもわかりやすい量子もつれの説明は数少ないです。
英語で量子もつれはQuantum Entanglement(クウォンタム・エンタングルメント)と呼ばれます。量子コンピューターの研究開発の話の中などによく出て来るため、最近量子もつれという言葉を耳にすることも多いのかもしれません。
でも、量子もつれという現象自体は、それほど新しいものではありません。この現象を巡る様々な議論は、アインシュタインやボアの時代からなされています。量子もつれについて色々調べていたときに、なかなか適度な中身がありつつもわかりやすい説明がなされたものが見つからなかったので、この記事では文系の知識でもわかるように量子もつれについて、わかりやすく説明してみたいと思います。
量子もつれとは何か
量子の振る舞いは波動関数で記述される
電子や光子と行った小さな粒子の振る舞いは、波動関数と呼ばれる関数の式によって記述されることについては以下の記事に書かせていただきました。簡単に言うと、粒子の振る舞いは実際に観測されるまではっきりと知ることは出来ませんが、波動関数からある粒子がある状態にある確率を導くことが出来るというものです。
もつれた量子とは何か
量子もつれとは言ったものの、そもそも「量子がもつれる」というのは一体どういうことなのでしょう?
小さな粒子である1つの量子の振る舞いは、上記の通り1つの波動関数で記述されるわけですが、1つの波動関数で記述することのできる複数の量子を作るということが可能です。1つの波動関数で記述される2つの量子が、もつれた量子のペアです。
確率的な「はず」の量子の世界
この2つの量子の振る舞いは、どちらも同じ波動関数で記述することができるわけですが、波動関数から私たちが知ることの出来る量子の状態というのは確率的なものでしたね。つまり、実際に測定してみるまで、量子が実際にどんな状態にあるかはわからないはずなのです。
例えば、量子は「スピン」と呼ばれる固有の量を持っています。ある量子のスピンの方向は、実際に測定されるまで波動関数が許す「全ての方向」であり、実際に測定して初めてその量子のスピンの方向がわかるということになります。
2つのもつれた量子のスピンを測定するとき、2つの量子は同じ波動関数を持つという以上の関連はありません。見えない糸で繋がっているというわけではなくそれぞれ個別の粒子です。よって測定がなされるまで、2つの量子のスピンの方向はそれぞれ「全ての方向」であるということになります。
重ね合わせ(Superposition)
ここでスピンの方向が「全ての方向」であるというのが実際どういう状態なのか、わかりにくいですよね。これは私たちの経験でイメージできるものとは少し異なっています。どの方向にも収束する可能性を持っているということで、全ての方向のスピンが重なった状態と考えて「重ね合わせ」の状態と呼ばれます。
スピンを測定すると不思議な結果になる
スピンの測定に当たって、垂直方向の測定をするとしましょう。すると、それぞれの量子は上向きのアップか、あるいは下向きのダウンかどちらかの方向に収束します。アップになるかダウンになるかの確率は50%ずつです。よって2つの量子を測定したときの結果としては、2つともアップ、片方がアップでもう一方がダウン、2つともダウンという3種類の可能性が考えられますね。
ところが、実際に測定してみると、もつれた2つの量子は必ず、片方がアップだともう一方がダウンになるのです!
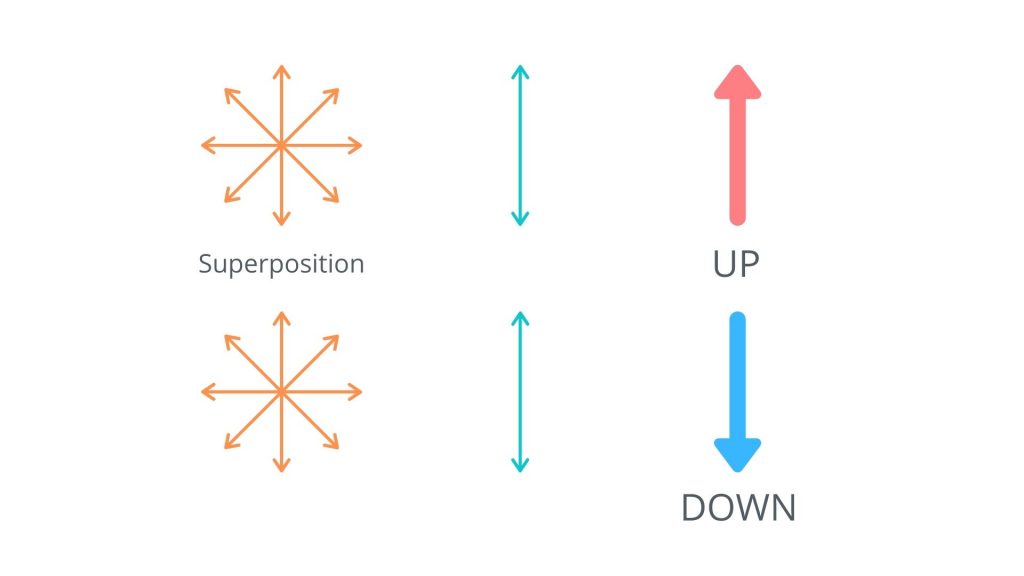
2つのもつれた量子のペアが、どれほど離れた場所にあっても、同時に2つの量子のスピンを測定すると必ずこのような測定結果になります。繰り返しますが、量子の状態は波動関数で表されていて、実際に測定してみるまでその状態は確率的にしかわからないはずです。また、2つの量子の振る舞いは同じ波動関数で記述されますが、それぞれは個別の粒子です。
それなのに、片方の量子の測定結果をもう一方の量子が瞬時に知ることができたかのように、量子のペアはお互いに異なるスピンの方向を示すのです。
EPRパラドックス
非局所性(Non-Locality)
2つの量子の測定が近で行われたのであれば、片方の量子の測定結果の情報がとても速いスピードでもう一方の量子に伝わったと考えることもできます。
でも2つの量子の測定が十分に離れた場所で行われると、片方の量子の測定結果をもう一つの量子が瞬時に知ることができないことは明らかです。なぜなら相対性理論によると、何ものも光の速度を越えることはできないため、2つの量子がお互いの測定結果の情報を瞬時に伝達できるような手段はないからです。
それにも関わらず、この量子もつれによる測定結果の相関関係は、どれほど離れた場所でも起こります。伝わらないはずの情報が奇妙にも伝わっているかのような現象が起きるのです。これをアインシュタインは「不気味な遠隔作用(Spooky action at a distance)」と呼びました。
このような量子に関する情報は光の速度よりも速く伝わるという性質を利用して、従来のコンピューターよりも情報処理の速い量子コンピューターの可能性が見えるわけですね。
隠れた変数理論(Hidden Variable Theory)
アインシュタインは、この遠隔作用について説明できるメカニズムがあると主張しました。もし、もつれた量子のペアのそれぞれに、初めからある結果になる性質が備わっているとしたら、測定結果に必ず相関関係が現れることも説明できますね。
例えば、量子のペアの片方には初めから「測定されるとスピンがアップになる」という性質があり、もう一方には「測定されるとスピンがダウンになる」という性質が備わっているとします。すると、測定してみたときに片方がアップで、もう一方がダウンになるというのは、当たり前ということになりますね。情報が伝わらなくても最初からそうなると決まっていたので、測定するとアップとダウンになる言えるわけです。
このように初めから量子に与えられている性質を「隠れた変数」として、この考え方は隠れた変数理論と呼ばれます。
ベルの実験
アインシュタインはこの考え方を生涯買えなかったわけですが、1964年、隠れた変数理論が正しいかどうかを判断する実験をジョン・ベルというアイルランド人の物理学者が考案します。ベルの実験は、スピンではなく偏光についての測定によるものなので、まずは偏光について少し見ておきましょう。
偏光とは
光が偏光サングラスのような偏光フィルターを通ることについて考えます。先ほどのスピンの測定と同様に、光子は測定されるまであらゆる方向に振動しています。1つの光子の一部分だけがフィルターを通るということはないので、フィルターを通すという測定をすると、光子は通過するか、あるいはブロックされるかどちらかの結果が得られます。
光子の偏光は360度どの方向についても測定することができ、フィルターを通すことで光子の振動の方向を知ることができるというわけです。フィルターを通る前は全ての方向に振動しているわけですが、垂直方向のフィルターを通過したのであれば垂直方向の振動を、あるいは水平方向のフィルターを通過したのであれば水平方向の振動をしていると知ることができます。
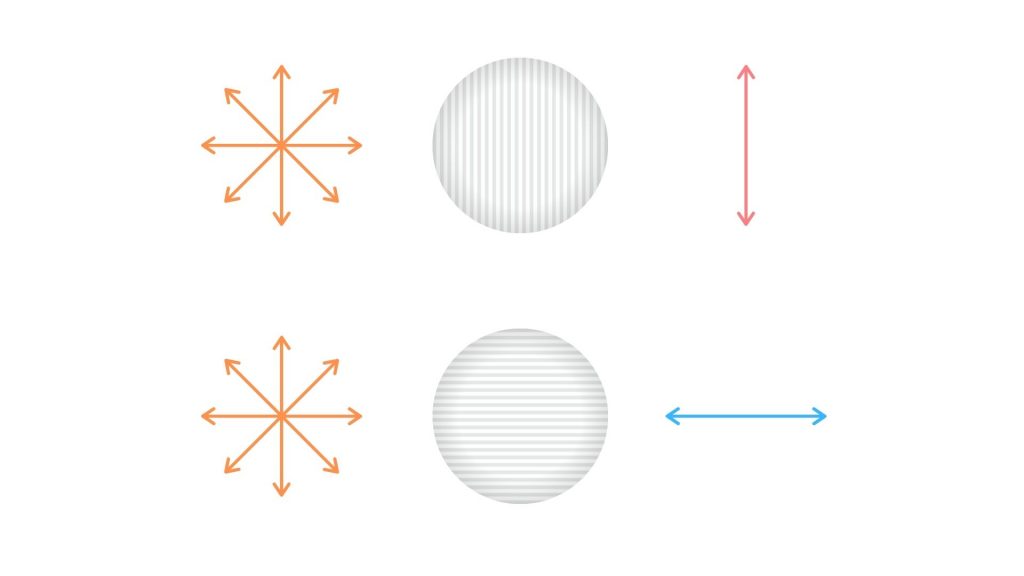
測定前は全ての方向に振動しているということは、ある光子についてもし異なる方向のフィルターで測定が行われたのであれば、そのフィルターを通る可能性もあったということになります。でも実際に私たちにわかるのは、測定をしたフィルターを通過したか、しなかったかの2つに1つです。
こうして偏光フィルターを通すと、ある方向に振動する光だけを通過させることができます。サングラスの場合はこの作用によって、水面で反射する光など視界を妨げる様々な方向に振動する光をブロックすることができるわけですね。
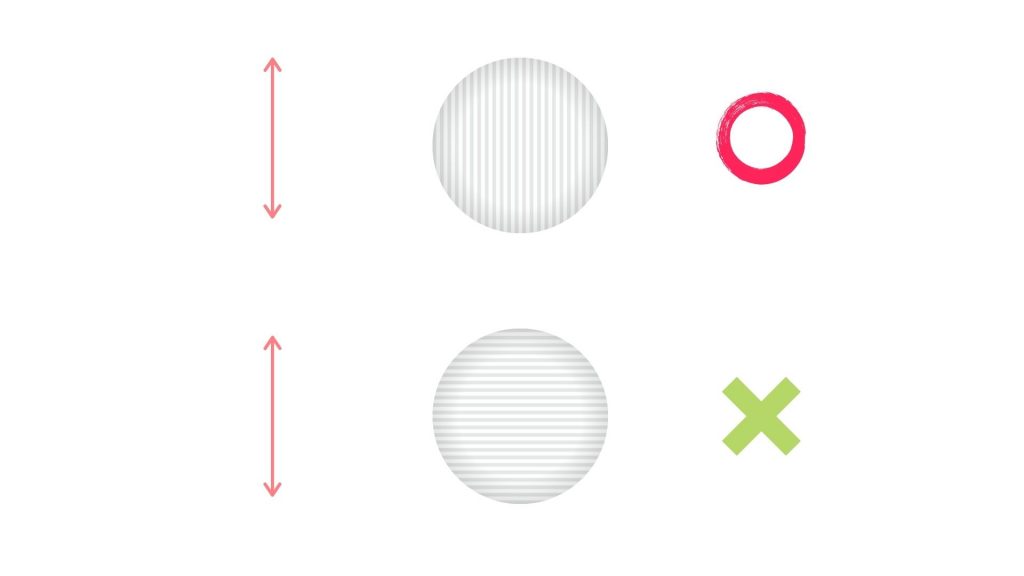
今度は、上記の垂直方向の偏光フィルターを通過した垂直方向に振動する光子が、もう1枚の偏光フィルターを通過することについて考えます。2枚目のフィルターが垂直方向であれば光は通り抜けることができますが、水平方向であれば光はブロックされてしまいます。このように、あるフィルターを通そうとしてブロックされてしまったものは、フィルターの方向に対して垂直方向に振動する光子と考えます。
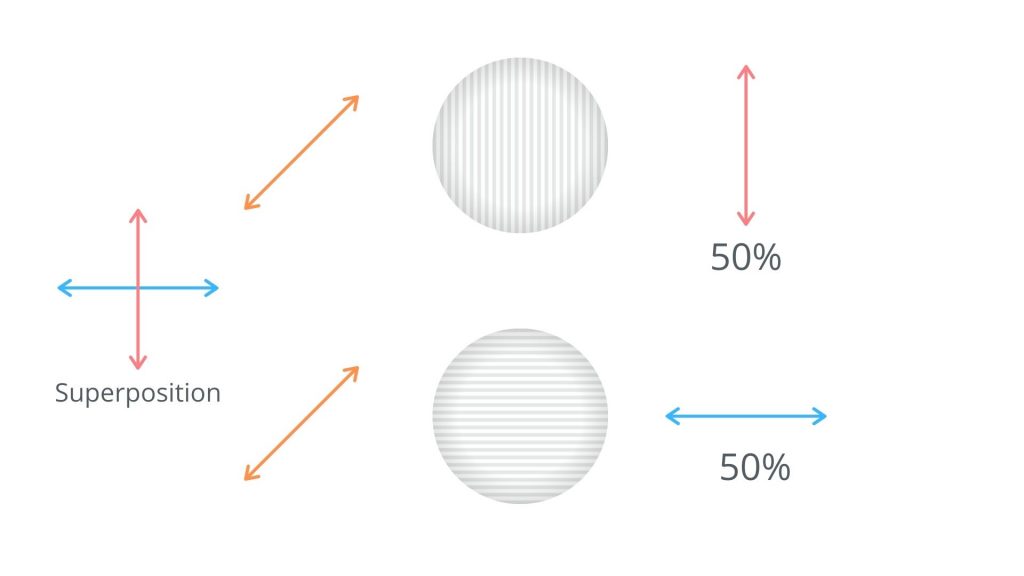
フィルターを通る光が斜め45度の方向に振動している場合はどうでしょうか?フィルターが垂直方向であっても、水平方向であっても、通過する確率は50%ずつです。斜めに45度の光は、垂直方向と水平方向の波の重ね合わせ(Superposition)として捉えることができるため、半々の確率で垂直方向にも、水平方向にも測定される可能性があります。でも、実際に測定すると、通過するかブロックするかのどちらかの結果に収束します。
もつれた光子の偏光の測定
量子もつれ状態にある2つの光子の偏光を測定することを考えます。2つの光子が同じフィルターを通ると、2つの測定結果は必ず同じになります。つまり、片方があるフィルターを通過すると、もう一方も同じフィルターを必ず通過します。片方がブロックされれば、もう一方も必ずブロックされます。
波動関数から私たちが知ることのできる光子の振る舞いは確率的であり、光子は測定されるまで全ての方向に振動しているので、フィルターを通過する確率とブロックさせる確率はそれぞれ50%ずつです。それなのに、2つの光子を同時にフィルターに通すと、偏光フィルターの方向がどんな向きであっても、同じ結果になるのです。
でも、もし量子のそれぞれが、初めからあるフィルターを通過するという性質を何らかの形で持っていたとしたらどうでしょう?そうすると2つの測定結果が同じになるということは、隠れた変数理論で説明できてしまいます。でも、量子もつれは、このような潜在する性質では説明のできない更に強い相関関係を示します。
ベルの実験
ベルが考えたのは、2つの量子の偏光を異なるフィルターで測定するという実験です。光子のペアの片方は、0度(垂直方向の)フィルター、あるいは45度のフィルターのどちらかの測定が行われ、ペアのもう一方は22.5度のフィルター、あるいは67.5度のフィルターで測定されます。測定結果は通過した(+1)か、しなかったか(-1)のどちらかで記録されます。
こうして十分にたくさんの光子のペアのそれぞれについて2枚のフィルターのどちらかで測定していくと以下の表のような結果が得られます。
| 0度 | 45度 | 22.5度 | 67.5度 | |
| ペア1 | +1 | +1 | ||
| ペア2 | -1 | +1 | ||
| ペア3 | +1 | -1 | ||
| ペア4 | -1 | -1 | ||
| ・・・ |
この実験結果の統計を取ってみると、以下のような割合になります。
| 22.5度を通過した | 67.5度を通過した | |
| 0度を通過した | 85% | 15% |
| 45度を通過した | 85% | 85% |
これはなぜかというと、2つのフィルターの作る角度が22.5度のとき、片方のフィルターを通過した光子と同じ偏光をもつ光子がもう一方のフィルターを通過する確率は、2つの角度のコサインの2乗で与えることができるからです。つまり、0度のフィルターを通る光子が22.5度のフィルターを通る確率は85%ということになります。これは先ほど45度の振動の光子の例で見たように、垂直方向に振動する光子は22.5度と67.5度の重ね合わせと見ることができるからです。
$$cos^2(22.5°)≈0.85$$
$$cos^2(67.5°)≈0.15$$
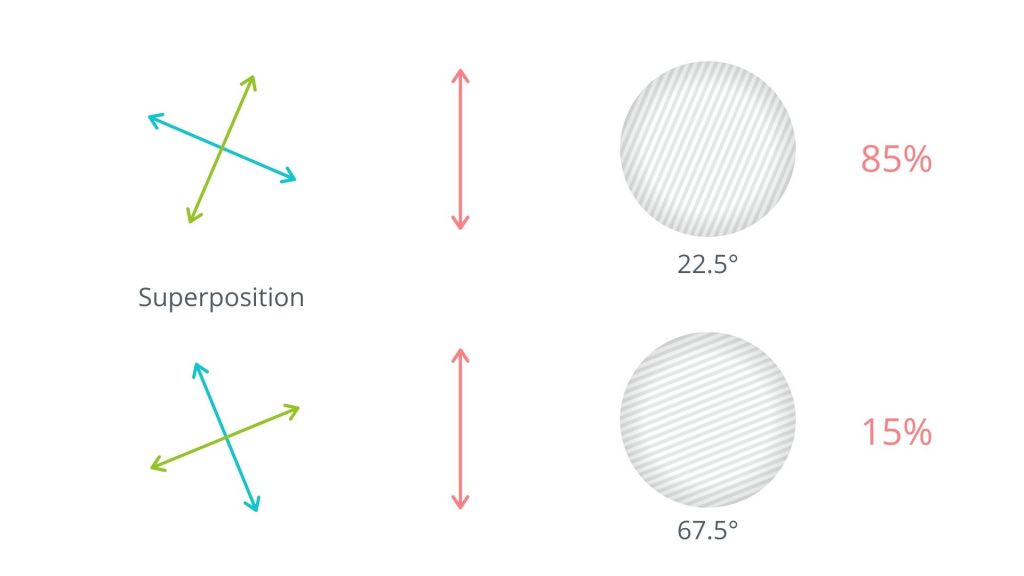
ところが、この実験結果について隠れた変数を割り当てようとすると問題が起こります。まず、22.5度のフィルターを通過するという性質を持った光子が100個あるとします。そのうち45度のフィルターも通過する性質を持っているのは85個です。22.5度のフィルターを通過する性質を持つ100個の光子のうち、67.5度のフィルターも通過するのは50個です。
すると、22.5度と45度の両方のフィルターを通過した85個のうち、67.5度のフィルターも通るのは50個となりますが、そうすると45度のフィルターと67.5度のフィルターを通過して22.5度のフィルターを通過しない光子の数は35個になり、45度と67.5度のフィルターを両方通過する光子の数と、45度フィルターを通過して67.5度を通過しない光子の数のバランスが取れません。
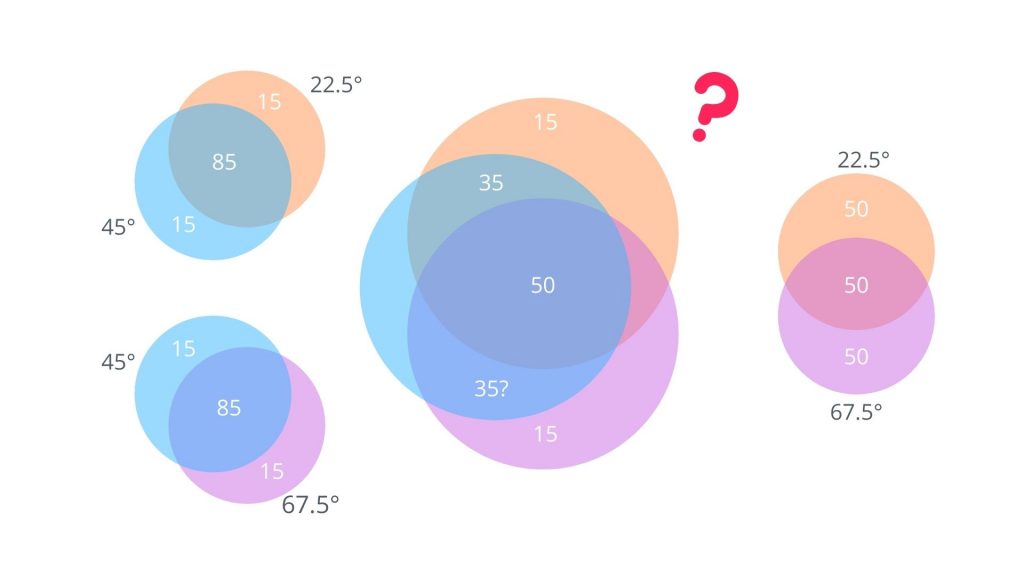
この割り当てがうまくいくのは以下の場合ですが、測定結果は以下のような割合になっていません。よって隠れた変数理論で量子もつれを説明することができないということになります。
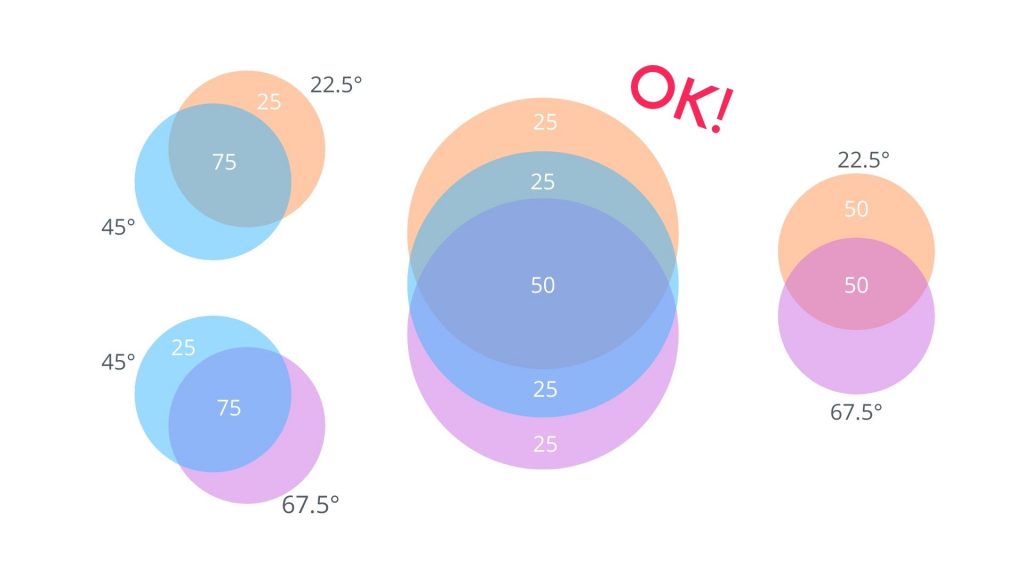
測定結果のような割合になるためには、隠れた変数では説明することのできない、片方の光子の測定結果の情報が、もう一方の光子に伝わる必要があります。
1つの光子が2枚のフィルターを続けて通り抜けるとき、最初のフィルターを通り抜けて垂直方向の振動の光子は、22.5度の2枚目のフィルターを通る確率は85%です。1つの光子が2枚のフィルターを通るのと同じことが、もつれた光子のペアで起こっています。つまり片方が通過したフィルターの測定結果がもう一方に伝わることによって、もう一つの光子の測定結果が変わるということです。
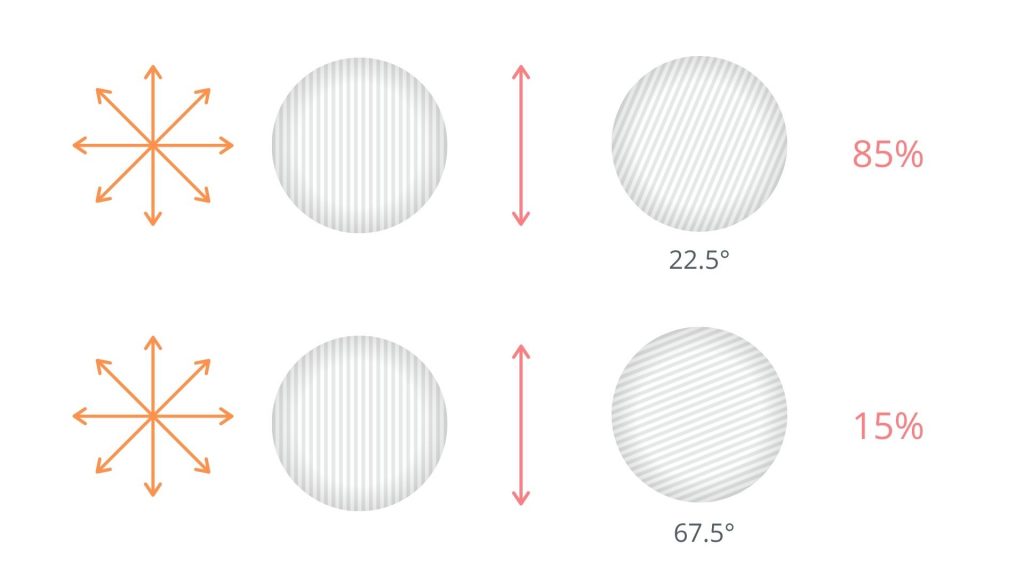
ベルの実験は歴史的に、光子のペアがお互いに情報交換をする術がないよう、様々な工夫を凝らした実験が行われてきました。そのどの結果も、隠れた変数理論では説明のつかない強い相関関係を示しています。よって、量子もつれは何か私たちの気づいていない理由によって起こっている現象ではなく、量子の性質の一つとして受け止めざるを得ない事象として考えられているのです。




